<aside> 📘 Series:

</aside>

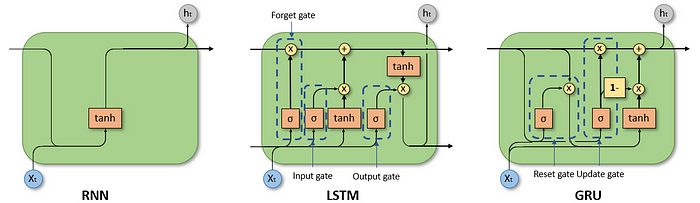
RNN, LSTM, and GRU cells.

If you want to make predictions on sequential or time series data (e.g., text, audio, etc.) traditional neural networks are a bad choice. But why?

In time series data, the current observation depends on previous observations, and thus observations are not independent from each other. Traditional neural networks, however, view each observation as independent as the networks are not able to retain past or historical information. Bascially, they have no memory of what happend in the past.

This led to the rise of Recurrent Neural Networks (RNNs), which introduce the concept of memory to neural networks by including the dependency between data points. With this, RNNs can be trained to remember concepts based on context, i.e., learn repeated patterns.

But how does an RNN achieve this memory?

RNNs achieve a memory through a feedback loop in the cell. And this is the main difference between a RNN and a traditional neural network. The feed-back loop allows information to be passed within a layer in contrast to feed-forward neural networks in which information is only passed between layers.

RNNs must then define what information is relevant enough to be kept in the memory. For this, different types of RNN evolved:

Traditional Recurrent Neural Network (RNN)
Long-Short-term-Memory Recurrent Neural Network (LSTM)
Gated Recurrent Unit Recurrent Neural Network (GRU)

In this article, I give you an introduction to RNN, LSTM, and GRU. I will show you their similarities and differences as well as some advantages and disadvantges. Besides the theoretical foundations I also show you how you can implement each approach in Python using tensorflow.

Recurrent Neural Network (RNN)

Through the feedback loop the output of one RNN cell is also used as an input by the same cell. Hence, each cell has two inputs: the past and the present. Using information of the past results in a short term memory.

For a better understanding we unroll/unfold the feedback loop of an RNN cell. The length of the unrolled cell is equal to the number of time steps of the input sequence.

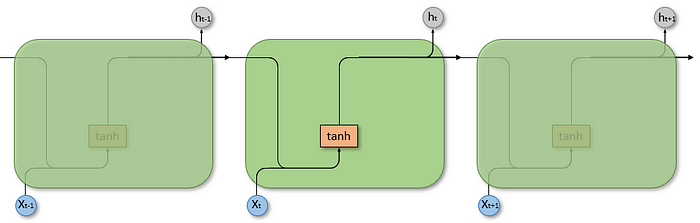
Unfolded Recurrent Neural Network.

We can see how past observations are passed through the unfolded network as a hidden state. In each cell the input of the current time step x (present value), the hidden state h of the previous time step (past value) and a bias are combined and then limited by an activation function to determine the hidden state of the current time step.

$$ h_t = \tanh(W_xx_t + W_hh_{t-1} + b) $$